计算机视觉中常见几何原理总结

问题描述

各种几何变换、几何原理傻傻分不清楚？进来看总结。

常见几何原理大分类

• 平面几何(2D->2D)
• 立体几何(3D->3D)
• 投影几何(3D->2D)
• 对极几何(2D<-3D->2D)
• 多视几何(3D->…->2D)

平面几何(2D->2D)

2D 图像常见的变换如下图所示：

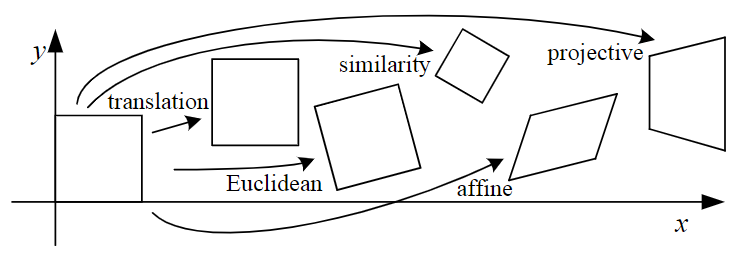
这些几何变换的数学性质如下表所示：

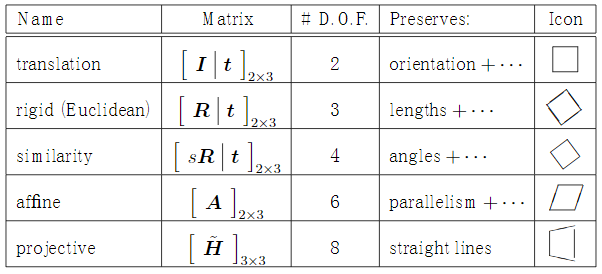
对极几何(2D<-3D->2D)

• Essential Matrix（本质矩阵）

  是什么：描述标定情况下的双目对极约束关系: ${x_2}^TEx_1=0$，其中: $E=\hat{T}R$；

  性质：自由度为5（旋转和平移一共6个自由度，尺度等价性，自由度减1）；秩为2（$\hat{T}$ 的秩为2）；

  怎么求：求解本质矩阵这一非线性优化问题，可以先优化对应线性最小二乘问题，再将线性解投影到5维本质流形上；也可以直接做非线性优化。特别地，对于已知5对匹配点，求解本质矩阵对应的非线性方程组属于 Kruppa 方程。

• Fundamental Matrix（基础矩阵）

  是什么：描述未标定情况下的双目对极约束关系: ${p_2}^TFp_1=0$，其中: $F=K^{-T}\hat{T}RK^{-1}$；

  性质：自由度为7（3x3矩阵一共9个元素，尺度等价性，自由度减1；秩为2，行列式为0，自由度再减1）；秩为2（$\hat{T}$ 的秩为2）；

  怎么求：求解基础矩阵这一非线性优化问题，可以先优化对应线性最小二乘问题，再将线性解投影到7维基础流形上；也可以直接做非线性优化。特别地，对于已知7对匹配点，求解基础矩阵对应的非线性方程组属于 Kruppa 方程。