Jcboxq

圆内均匀随机采样

 
  • Mar 20, 2022

问题描述

如何实现圆内均匀随机采样？

解决思路

  1. 直觉方法：在极坐标系下先后对方位角和距离进行均匀随机采样；
  2. 直觉方法错在只考虑了抽象出来的具体点被采概率相等，而没有考虑原始要求是点构成的区域内概率密度处处相等，如图：
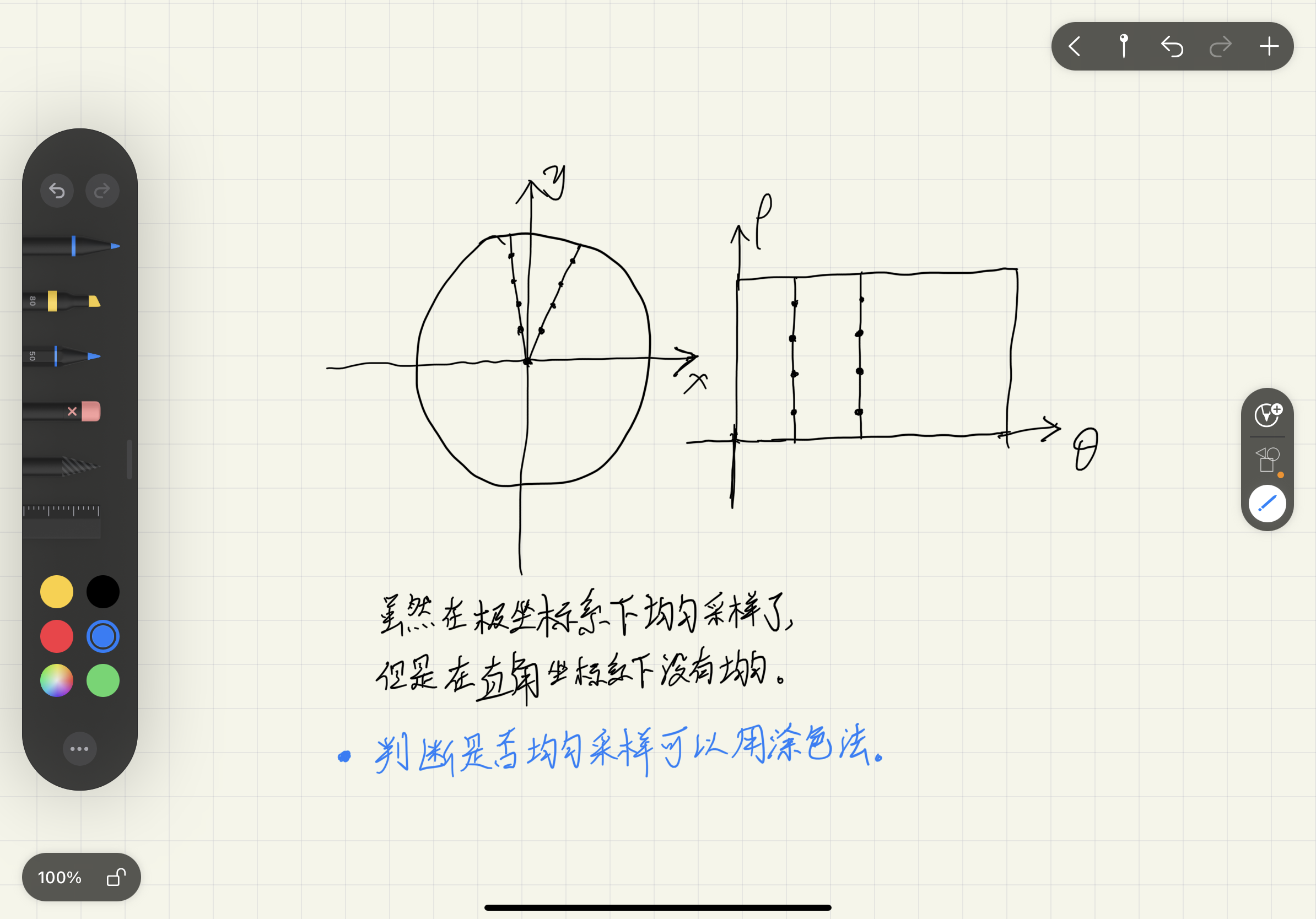
  1. Rejection Sampling(拒绝采样)：在圆的外切矩形中均匀随机采样，拒绝不在圆内的采样点。此方法实现简单，但是效率低。
  2. 反函数法：圆面积的公式为 $S=\pi r^2$，假如随机点要在圆内均匀分布，应该是每单位的面积点的数量要相同，即数量要和面积呈正比。因此半径方向累积概率分布函数与 $r^2$ 成正比：$F(r)=kr^2$，根据边界条件，可得 $k=\frac{1}{R^2}$。考虑到累积概率分布函数(CDF)的反函数可以用来生成符合对应概率密度函数(pdf)的随机分布，令 $r=F^{-1}(x)=R\sqrt{x}$，其中 $x$ 是[0,1]区间内均匀分布的随机数。
  3. 代码实现： 
     def GenCircleRandomPts(r, pt_cnt):        
     x_list = []
     y_list = []
     for k in range(pt_cnt):
         #首先生成角度theta [0,2*pi]
         random_theta = random.random() * math.pi * 2
         #生成距离圆心的长度
         random_r = math.sqrt(random.random()) * r
         x = math.cos(random_theta) * random_r
         y = math.sin(random_theta) * random_r
         x_list.append(x)
         y_list.append(y)
     return [x_list, y_list]

参考

  1. 知乎专栏
Search